Innføring til lineær regresjon

from sklearn.linear_model import LogisticRegression, LinearRegression
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from scipy.special import expit
from scipy.stats import expon
import math
! pip install statsmodels

Defaulting to user installation because normal site-packages is not writeable
Requirement already satisfied: statsmodels in /home/eirikgr/.local/lib/python3.9/site-packages (0.14.1)
Requirement already satisfied: numpy<2,>=1.18 in /home/eirikgr/.local/lib/python3.9/site-packages (from statsmodels) (1.26.0)
Requirement already satisfied: scipy!=1.9.2,>=1.4 in /home/eirikgr/.local/lib/python3.9/site-packages (from statsmodels) (1.11.4)
Requirement already satisfied: pandas!=2.1.0,>=1.0 in /home/eirikgr/.local/lib/python3.9/site-packages (from statsmodels) (2.1.1)
Requirement already satisfied: patsy>=0.5.4 in /home/eirikgr/.local/lib/python3.9/site-packages (from statsmodels) (0.5.6)
Requirement already satisfied: packaging>=21.3 in /home/eirikgr/.local/lib/python3.9/site-packages (from statsmodels) (23.2)
Requirement already satisfied: python-dateutil>=2.8.2 in /storage/software/easybuild/software/Python/3.9.6-GCCcore-11.2.0/lib/python3.9/site-packages (from pandas!=2.1.0,>=1.0->statsmodels) (2.8.2)
Requirement already satisfied: pytz>=2020.1 in /storage/software/easybuild/software/Python/3.9.6-GCCcore-11.2.0/lib/python3.9/site-packages (from pandas!=2.1.0,>=1.0->statsmodels) (2021.1)
Requirement already satisfied: tzdata>=2022.1 in /home/eirikgr/.local/lib/python3.9/site-packages (from pandas!=2.1.0,>=1.0->statsmodels) (2023.3)
Requirement already satisfied: six in /storage/software/easybuild/software/Python/3.9.6-GCCcore-11.2.0/lib/python3.9/site-packages (from patsy>=0.5.4->statsmodels) (1.16.0)

Introduksjon

La oss definere en lineær modell \(Y = \beta_0 + \beta_1X + \epsilon\) med \(\beta_0 = 2\) og \(\beta_1\) = 3. La oss anta først at \(\epsilon\) representer en tilfeldig, normalfordelt (\(\mu = 0\)), feil.

# Antall verdier av Y
npoints = 400
# Standardavviket vi bruker når vi trekker tilfeldige tall for feilen
sigma_e = 2

x = np.linspace(0, 2, npoints)
# Den sanne modellen (population regression line)
Y_pop_reg = 2 + 3*x

mean = np.zeros(npoints)
std = np.ones(npoints)*sigma_e

# Tilfeldige punkter
Y = 2 + 3*x + np.random.normal(mean,std)

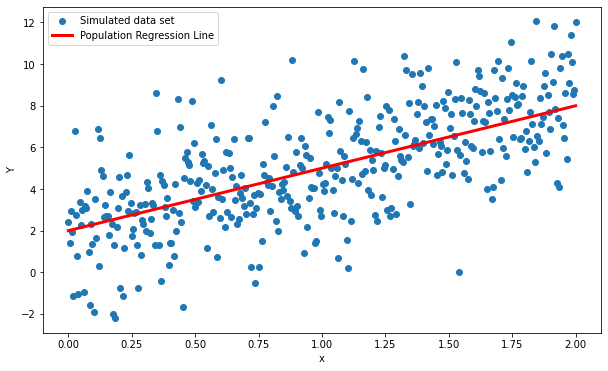
La oss se hvordan de 400 punktene av \(Y\) fordeler seg i forhold til den sanne modellen.

plt.figure(1, figsize=(10, 6))
plt.clf()
plt.scatter(x,Y,label="Simulated data set")
plt.plot(x, Y_pop_reg, label="Population Regression Line", color="red", linewidth=3)
plt.xlabel("x")
plt.ylabel("Y")
plt.legend()

<matplotlib.legend.Legend at 0x7fb0bb1f6580>

Så prøver vi oss på en lineær regresjon av punktene. Men først må vi manipulere input-vektorene litt.

Siden funksjonen vi vil bruke for å tilpasse en enkel lineær regresjons til dataene våre kun inneholder én predikator så må vi legge til en ekstra dimensjon for at funksjonen ikke klager. I praksis vil det si å konvertere en vektor til en matrise med èn ekstra dimensjon. Man kan enkelt sjekke dimensjonen til et numpy-array object i pyhon ved å kalle på shape, den gir deg eksakt dimensjonene av arrayen. Før vi legger til en dimensjon:

x.shape

(400,)

x_lr = x[:, np.newaxis]
Y_lr = Y[:, np.newaxis]

… og etterpå

x_lr.shape

(400, 1)

clf = LinearRegression().fit(x_lr,Y_lr)

print("Coefficient = %.2f"%clf.coef_[0])
print("Intercept = %.10f"%clf.intercept_[0])
print("Score/R^2 = %.2f"%clf.score(x_lr,Y_lr))

Coefficient = 3.23
Intercept = 1.8487772932
Score/R^2 = 0.46

/tmp/ipykernel_2222527/4082072972.py:1: DeprecationWarning: Conversion of an array with ndim > 0 to a scalar is deprecated, and will error in future. Ensure you extract a single element from your array before performing this operation. (Deprecated NumPy 1.25.)
  print("Coefficient = %.2f"%clf.coef_[0])

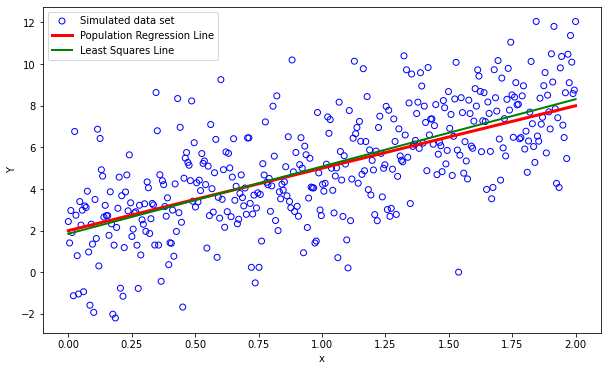
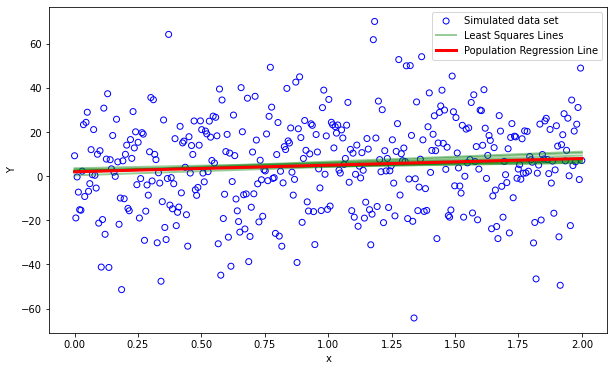
La oss se hvordan tilpasningen passer med populasjonen

fit_lr = clf.intercept_[0] + clf.coef_[0]*x
plt.figure(1, figsize=(10, 6))
plt.clf()
plt.scatter(x,Y,label="Simulated data set",facecolors='none', edgecolors='b')
plt.plot(x, Y_pop_reg, label="Population Regression Line", color="red", linewidth=3)
plt.plot(x, fit_lr, label="Least Squares Line", color="green", linewidth=2)
plt.xlabel("x")
plt.ylabel("Y")
plt.legend()

<matplotlib.legend.Legend at 0x7fb0bb1768e0>

Tilpasse flere modeller med tilfeldige feil

For å vise at dersom vi gjentar forsøket med å generere nye datatsett for den tilfeldige variabelen \(Y\) kan vi observere:

1. at det er ingen bias i least square estimatene våre

2. sample mean er en god approksimasjon til den sanne populasjonen

3. \(\sigma = \sqrt{\left(\frac{RSS}{n-1}\right)}\) er lik variansen i \(Y\) gitt ved \(Var(\epsilon)\)

La oss se på 10000 tilfeldige utvalg av \(Y\) hvor vi kan endre standardavviket til normalfordelingen vi trekker feilen fra.

import statsmodels.api as sm 
n = 10000
npoints = 400
beta0 = np.zeros(n)
beta1 = np.zeros(n)
muhat = np.zeros(n)
sigma = np.zeros(n)
rsquared = np.zeros(n)
fits = []
x = np.linspace(0, 2, npoints)
Y_pop_reg = 2 + 3*x

mean = np.zeros(npoints)
std = np.ones(npoints)*20

for i in range(n):
    Y = 2 + 3*x + np.random.normal(mean,std)
    x_lr = x[:, np.newaxis]
    Y_lr = Y[:, np.newaxis]
    
    x_lr_ac = sm.add_constant(x_lr)
    clf = sm.OLS(Y_lr,x_lr_ac).fit() 
    
    fit_lr = clf.params[0] + clf.params[1]*x
    
    sigma[i] = np.sqrt(clf.ssr/(len(x)-2))
    
    if i%(n/10) == 0:
        fits.append(fit_lr)
    
    beta0[i] = (clf.params[0])
    beta1[i] = (clf.params[1])
    muhat[i] = np.mean(fit_lr)
    rsquared[i] = clf.rsquared

Konverter en liste til numpy-array for plotting

fits_lr = np.asarray(fits, dtype=np.float32)

La oss plotte de ulike parameterne fra hver av tilpasningene til \(Y\)

plt.figure(1, figsize=(10, 6))
plt.clf()
plt.hist(beta0,bins=100, label=r'$\beta_0$', color="red", linewidth=3,alpha=.4);
plt.hist(beta1,bins=100, label=r'$\beta_1$', color="green", linewidth=3,alpha=.4);
plt.hist(muhat,bins=100, label=r'$\hat{\mu}$', color="blue", linewidth=3,alpha=.4);
plt.hist(sigma,bins=100, label=r'$\sigma$', color="yellow", linewidth=3,alpha=.4);
plt.legend()

<matplotlib.legend.Legend at 0x7fb0b8bdb2b0>

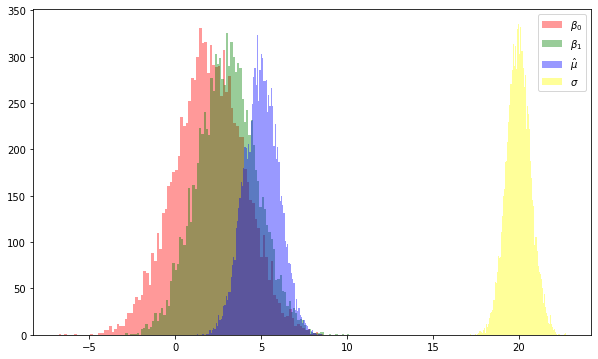
Dette plottet er som forventet. De to parameterne, \(\beta_0\) og \(\beta_1\), er sentrert rundt den sanne verdien (2 og 3 hhv.). Vi vet at \(\sigma^2 = Var(\epsilon)\). Siden vi trekker feilen \(\epsilon\) for hvert eksperiment fra en normalfodeling med standardavvik 8 så samsvarer det godt med det vi observerer over.

Videre kan vi se på \(\hat{\mu}\) som er vårt estimat av sample mean/population mean (vi antar at sample mean er en god approksimasjon til population mean). Dersom vi ser på kun et av “eksperimentene” så vil \(\hat{\mu}\) over- eller underestimere \(\mu\), men gjør vi nok eksperimenter så vil gjennomsnittlig \(\hat{\mu}\) være eksakt lik \(\mu\). Det er dette vi mener når vi sier at \(\hat{\mu}\) ikke er en forutinntatthet (biased) estimator. Samme gjelder for least square koeffisientene, \(\hat{\beta_0}\) og \(\hat{\beta_1}\), som vi ser har en gjennomsnittlig verdi som sammenfaller godt med de sanne verdiene for \(\beta_0\) og \(\beta_1\). Dette blir klart om vi ser på et utvalg av de tilfeldige trekningene av \(Y\)

plt.figure(1, figsize=(10, 6))
plt.clf()
plt.scatter(x,Y,label="Simulated data set",facecolors='none', edgecolors='b')
for i in range(len(fits_lr)-1):
    plt.plot(x, fits_lr[i], color="green", linewidth=2,alpha=0.4)
plt.plot(x, fits_lr[i], label="Least Squares Lines", color="green", linewidth=2,alpha=0.4)
plt.plot(x, Y_pop_reg, label="Population Regression Line", color="red", linewidth=3)
plt.xlabel("x")
plt.ylabel("Y")
plt.legend()

<matplotlib.legend.Legend at 0x7fb0b88ae9a0>

Videre kan vi regne ut standard feil på koeffisentene til least square tilpasningen vår gitt ved

\[SE(\hat{\beta_0})^2 = \sigma^2\left[\frac{1}{n} + \frac{\bar{x}^2}{\Sigma_{i=1}^{n}\left(x_i-\bar{x}\right)^{2}}\right]\]

og

\[SE(\hat\beta_1)^2 = \frac{\sigma^2}{\Sigma_{i=1}^{n}\left(x_i-\bar{x}\right)^2}\]

hvor \(\bar{x}\) er sample mean. La oss regne de ut:

se_beta0 = np.sqrt((np.mean(sigma)*np.mean(sigma))*((1/npoints) + ((np.mean(x)*np.mean(x))/np.sum((x-np.mean(x))*(x-np.mean(x))))))
se_beta1 = np.sqrt((np.mean(sigma)*np.mean(sigma))/(np.sum((x-np.mean(x))*(x-np.mean(x)))))

print("Standard feil i beta_0 = %.3f"%se_beta0)
print("Standard feil i beta_1 = %.3f"%se_beta1)

Standard feil i beta_0 = 1.994
Standard feil i beta_1 = 1.726

Spørsmål

1. Hva skjer med feilen på \(\beta_1\) dersom vi øker spredningen i \(x\)?

2. Hva skjer med feilen på koeffisentene dersom vi øker antall “eksperimenter”?

Feilene på estimatet av \(\beta_0\) og \(\beta_1\) over gir oss følgende konfidensintervall:

print("Det er 95%% sjanse for at intervallet [%.2f, %.2f] inneholder den sanne verdien av beta0 (2)"%(np.mean(beta0)-2*se_beta0,np.mean(beta0)+2*se_beta0))
print("Det er 95%% sjanse for at intervallet [%.2f, %.2f] inneholder den sanne verdien av beta1 (3)"%(np.mean(beta1)-2*se_beta1,np.mean(beta1)+2*se_beta1))

Det er 95% sjanse for at intervallet [-2.00, 5.98] inneholder den sanne verdien av beta0 (2)
Det er 95% sjanse for at intervallet [-0.43, 6.47] inneholder den sanne verdien av beta1 (3)

Hypotesetesting

Standardfeilen kan også brukes til å foreta hypotesetesting. La oss definere to hypoteser

\(H_0\) : det er ingen sammenheng mellom \(X\) og \(Y\)

\(H_a\) : det er noe sammenheng mellom \(X\) og \(Y\)

som i realiteten er et samme som å spørre om \(\beta_1 = 0\) eller om \(\beta_1 \neq 0\). Vi kan teste dette ved bruke t-statistikk gitt ved

\[t = \frac{\hat{\beta_1}-0}{SE(\hat{\beta}_1)}\]

Heldigvis har vi tilgang på t-statistikk metoder i statsmodels gjennom stats.t()

from scipy.stats import t
# La oss regne ut "vår" t fra standardfeilen
tval = np.mean(beta1)/se_beta1
# Lag en x-vektor (-10 til 10 skulle være mer enn nok)
xt = np.arange(-10,10,0.001)
print("t = %.3f"%tval)
# få tak i sannsynlighets tetthetsfunksjonen 
# til t-foredelingen (som er veldig lik 
# normalfordelingen ved antall frihetsgrader > 30)
tstat = t.pdf(xt,npoints-2)

t = 8.689

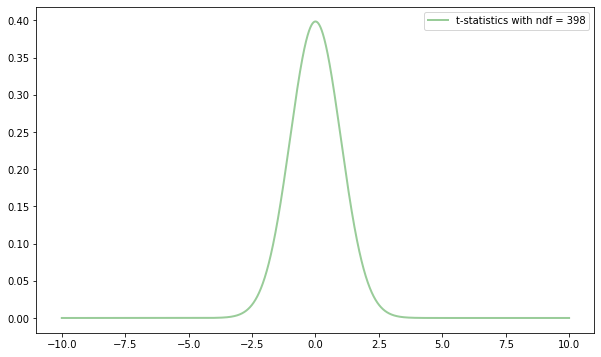
La oss ta en titt:

plt.figure(1, figsize=(10, 6))
plt.clf()
plt.plot(xt, tstat, label="t-statistics with ndf = %i"%(npoints-2), color="green", linewidth=2, alpha=0.4)
plt.legend()

<matplotlib.legend.Legend at 0x7fb0bb6502e0>

Det er til og med funksjoner til å regne ut konfidensintervall

t.interval(0.95,npoints-2)

(-1.9659423239761926, 1.9659423239761926)

Kjenner du igjen dette? (hint: \(\approx 2\))

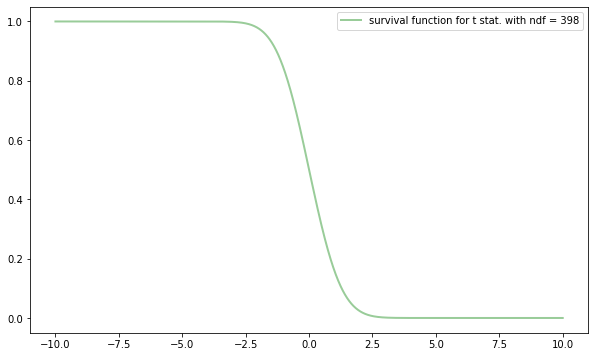
Vi kan deretter regne ut sannsynligheten for å observere en hvilken som helst t identisk til eller større enn \(|t|\). Med andre ord; vi må regne ut integralet i halene (dvs. tval < t < -tval) til fordelingen over. Det kan vi gjøre ved å bruke “overlevelsesfunksjonen” (survival function) til sannsynlighetsfunksjonen over. Kan enkelt hentes i statsmodels gjennom t.sf()

tsurv = t.sf(xt, npoints-2)

plt.figure(1, figsize=(10, 6))
plt.clf()
plt.plot(xt, tsurv, label="survival function for t stat. with ndf = %i"%(npoints-2), color="green", linewidth=2, alpha=0.4)
plt.legend()

<matplotlib.legend.Legend at 0x7fb0bb4ab820>

En enkel liten loop for å finne hvor vi skal starte integralet (som i realiteten er verdien til indeks x hvor vi krysser verdien for \(t\) som vi fant over)

prob = 0.0
j = -1
for i in xt:
    j += 1
    if i > tval:
        cutval = j
        break

Og så finn p-verdien

tsurv[cutval]

4.8097916554844284e-17

Ekstramateriale

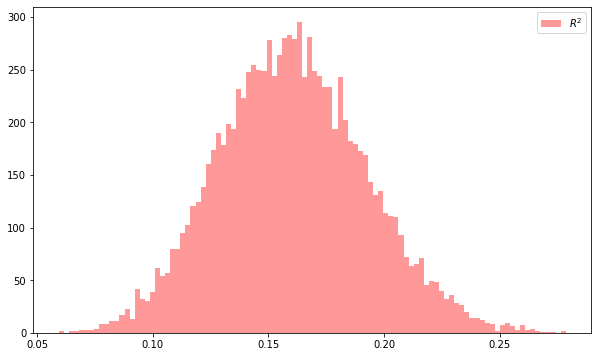
Hvor bra er tilpasningen vår? La oss se på de \(R^2\) for alle trekningene av \(Y\). Hva skjer dersom vi endrer variansen i feilen?

plt.figure(1, figsize=(10, 6))
plt.clf()
plt.hist(rsquared,bins=100, label=r'$R^2$', color="red", linewidth=3,alpha=.4);
plt.legend()

<matplotlib.legend.Legend at 0x7fb0bb41a3d0>