Lineær Regresjon (løsningsforslag til oppgave fra 22. januar)#
La oss fortsette med det klassiske datasettet som inneholder data om størrlsen (lende og bredde) av begerbladene (engelsk: sepal) (de ytre bladene i en blomst) og kronbladene (engelsk: petal) til tre ulike type Iris (setosa, versicolor og virginica) - på norsk hhv.: vill iris, praktiris og blått flagg iris). Vi skal bruke dette datasettet til å se nærmere på lineær regresjon. Først må vi importere noen pakker og lese inn datasettet.
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression, LinearRegression
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from scipy.special import expit
from scipy.stats import expon
import math
Datasettet er tilgjengelig direkte fra ScikitLearn
from sklearn import datasets
iris = datasets.load_iris()
df = pd.DataFrame(data= np.c_[iris['data'], iris['target']],
columns= iris['feature_names'] + ['target'])
df.head()
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | target | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | 0.0 |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | 0.0 |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | 0.0 |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | 0.0 |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | 0.0 |
Nå er typen iris lagret som 0, 1 og 2. Vi vil gjerne oversette dette til faktiske navn slik at vi ikke glemmer hva de ulike tallene betyr. Dette kan vi gjøre på flere måter, men en mulighet er å bruke såkalte lambda-funksjoner som utfører en test av hvert enkelt element in en kolonne.
df['species'] = df['target'].apply(lambda x: "setosa" if x == 0.0 else ("versicolor" if x == 1.0 else "virginica"))
Det er keitete å ha kolonnenavn som inneholder mellomrom så la oss lage nye enklere navn. Når vi setter inplace=True betyr det at data-framen df automatisk blir oppdatert med de nye kolonnenavnene. Hvis ikke må man bruke df = df.rename() for at endringene skal bli oppdatert.
df.rename({'sepal length (cm)': 'sepal_length'}, axis='columns',inplace=True)
df.rename({'sepal width (cm)': 'sepal_width'}, axis='columns',inplace=True)
df.rename({'petal length (cm)': 'petal_length'}, axis='columns',inplace=True)
df.rename({'petal width (cm)': 'petal_width'}, axis='columns',inplace=True)
df.head()
| sepal_length | sepal_width | petal_length | petal_width | target | species | |
|---|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | 0.0 | setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | 0.0 | setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | 0.0 | setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | 0.0 | setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | 0.0 | setosa |
Tilslutt, la oss droppe kolonnen med target siden vi når har laget en ny kolonne species som inneholder den samme informasjonen. Det gjør vi enkelt slik (merk at *axis=1” betyr at vi vil droppe en kolonne. Dersom vi ikke spesifiserer noe er axis satt til 0, dvs. at en hel rad blir fjernet.
df.drop(['target'],axis=1,inplace=True)
df.head()
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
Forberedelser til lineær regresjon#
Vi skal starte med å se om det er en sammenheng mellom lengde og bredde til begerbladene til Iris Setosa. Det første vi må gjøre er å trekke ut disse to kolonnene fra data-framen og konvertere de til numpy-vektorer. Det gjør vi ved hjelp av funksjonen to_numpy().
X_setosa_sepal_length = df[df["species"] == "setosa"].sepal_length.to_numpy()
X_setosa_sepal_width = df[df["species"] == "setosa"].sepal_width.to_numpy()
Naivt - uten at jeg på noen måte er biolog - vil jeg anta at det er en korrelasjon mellom lengde og bredde av begerbladene. La oss ta en titt på data-settet.
plt.scatter(df[df["species"] == "setosa"].sepal_length, df[df["species"] == "setosa"].sepal_width)
plt.xlabel("begerblad lengde [cm]");
plt.ylabel("begerblad bredde [cm]");
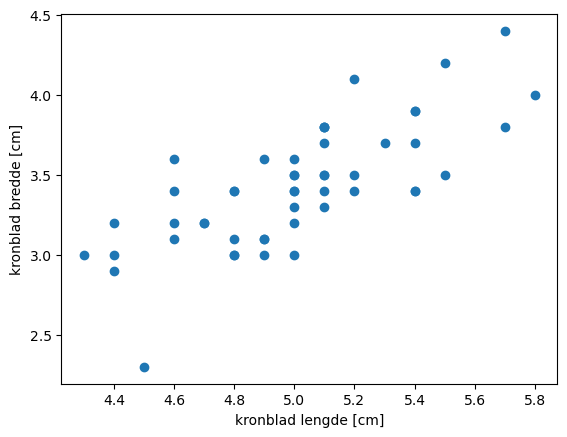
Ganske riktig! Det ser ut til å være en ganske klar sammenheng!
I prinsippet kan vi utføre multidimensjonal lineær regresjon. I dette tilfellet prøver vi derimot å predikere hva bredden til et kronblad vil være basert på en måling av lengden. Dette er det vi kaller enkel lineær regresjon hvor vi skal forutsi en respons (kronbladets bredde) basert på en enkelt predikator (kronbladets lengde). Vi antar altså at det er en lineær sammenheng mellom disse to verdiene som kan beskrives matematisk slik
\(Y \approx \beta_0 + \beta_1 X + \epsilon\)
Hvor Y i dette tilfellet er kronbladets bredde, X er det vi måler, altså kronbladets lengde. De to konstantene får vi ved å gjøre en tilpasning til treningsdataene våre ved å bruke minste kvadraters metode dvs. å minimere residual sum of squares (RSS). Verdiene for \(\beta_0\) og \(\beta_1\) som minimerer RSS skriver vi ofte med en hatt, \(\hat{\beta}_0\) og \(\hat{\beta}_1\). På samme måte skriver vi \(\hat{y}\) for å spesifisere at vi snakker om vår predksjon av Y. Vi kan da skrive
\(\hat{y} = \hat{\beta}_0 + \hat{\beta}_1 x\),
hvor \(x = X\)
Siden funksjonen vi vil bruke for å tilpasse en enkel lineær regresjons til dataene våre kun inneholder én predikator så må vi legge til en ekstra dimensjon for at funksjonen ikke klager. I praksis vil det si å konvertere en vektor til en matrise med èn ekstra dimensjon. Man kan enkelt sjekke dimensjonen til et numpy-array object i pyhon ved å kalle på shape, den gir deg eksakt dimensjonene av arrayen. Før vi legger til en dimensjon:
X_setosa_sepal_length.shape
(50,)
Vi legger til en ekstra dimensjon/akse:
X_setosa_sepal_length = X_setosa_sepal_length[:, np.newaxis]
X_setosa_sepal_width = X_setosa_sepal_width[:, np.newaxis]
… og vi får en ny dimensjon i arrayen vår. Dette vil bli mer intuitivt når vi skal se på tilfeller med flere predikatorer.
X_setosa_sepal_length.shape
(50, 1)
Lineær Regresjon#
scikit-learn har mange nyttige funksjoner for ulike typer maskinlæringsalgoritmer. De er i tillegg relativt godt dokumenterte - så her er det bare å slå seg løs. Vi skal nå bruke LinearRegression(). Den tar enkelt og greit som input repsons og predikatoren i form av numpy-arrayer. Funksjonen fit() setter i gang prosessen med å finne den beste tilpasningen til dataene våre.
clf = LinearRegression().fit(X_setosa_sepal_length,X_setosa_sepal_width)
Når den er ferdig kan vi hente ut veridene av \(\hat{\beta}_0\) (intercept) og \(\hat{\beta}_1\) (coef). Vi kan også få en første indikasjon på hvor bra tilpasningen er ved å skrive ut \(R^2\).
print("Coefficient = %.2f"%clf.coef_)
print("Intercept = %.2f"%clf.intercept_)
print("Score/R^2 = %.2f"%clf.score(X_setosa_sepal_length,X_setosa_sepal_width))
Coefficient = 0.80
Intercept = -0.57
Score/R^2 = 0.55
Eller
\(\hat{y} = -0.57 + 0.8x\)
Husk at score (eller \(R^2\)) er definert som
\begin{equation} R^2 = 1 - \frac{RSS}{TSS} \end{equation}
RSS (residual sum of squares) er definert som
og TSS (total sum of squares)
hvor \(\bar{y}\) er det globale gjennomsnittet i dataene våre.
\(R^2\) er et mål på hvor mye av variasjon i Y som kan beskrives ved X. Dersom \(R^2\) er nære 1 betyr det at en stor del av variasjonen i Y kan beskrives av regresjonsanalysen. Om den derimot er nære 0 betyr det at regresjonsanalysen i liten grad evner å beskrive variasjonen i responsen (Y). Det betyr
at den lineære modellen er feil
at variansen til feilen, \(\epsilon\), \(\sigma^2 = Var(\epsilon)\) er for høy
evt. begge deleer.
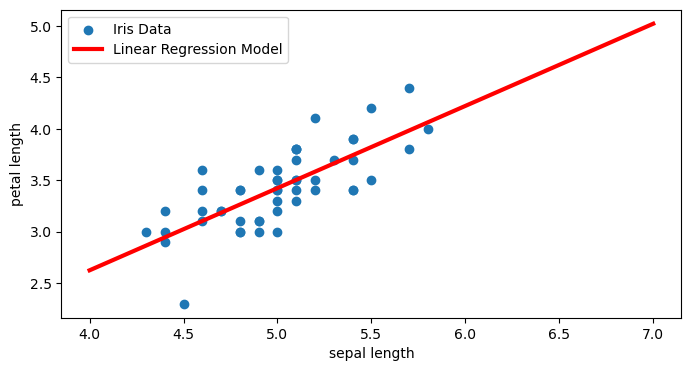
La oss uansett se hvordan den lineære modellen ser ut når vi plotter den sammen med datapunktene.
# Definer en x-vektor som dekker datapunktene (i dette tilfellet mellom 4 og 7 cm)
X_plot = np.linspace(4, 7, 300)
# Lag så responsfunksjonen ved å bruke parameterne fra modellen vår
fit = clf.intercept_[0] + clf.coef_[0]*X_plot
plt.figure(1, figsize=(8, 4))
plt.clf()
plt.scatter(df[df["species"] == "setosa"].sepal_length, df[df["species"] == "setosa"].sepal_width,label="Iris Data")
plt.plot(X_plot, fit, label="Linear Regression Model", color="red", linewidth=3)
plt.xlabel("sepal length")
plt.ylabel("sepal width")
plt.legend()
<matplotlib.legend.Legend at 0x7ff0941e2e50>
Alternativ framgangsmåte#
Vi kan også bruke et annet bibliotek i python (statsmodels) som er et godt alternativ til scikit-learn om vi enkelt vil hente ut enda mer informasjon om modellen vår. Da må vi starte med å importere denne
import statsmodels.api as sm
Vi kan bruke OLS (ordinary least square) på samme måte som vi brukte scikit-learn metoden over. Den gir oss da tilgang til enda mer informasjon om modellen. Merk at intercept/\(\beta_0\) ikke er inkludert i standard-oppsettet i statsmodels.ols() og derfor eksplisitt må legges til ved å bruke sm.add_constant() på respons-vektoren.
X_setosa_sepal_length_const = sm.add_constant(X_setosa_sepal_length)
model = sm.OLS(X_setosa_sepal_width,X_setosa_sepal_length_const).fit()
#display model summary
print(model.summary())
# residual sum of squares
print(model.ssr)
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.551
Model: OLS Adj. R-squared: 0.542
Method: Least Squares F-statistic: 58.99
Date: Fri, 26 Jan 2024 Prob (F-statistic): 6.71e-10
Time: 09:53:01 Log-Likelihood: -1.9002
No. Observations: 50 AIC: 7.800
Df Residuals: 48 BIC: 11.62
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const -0.5694 0.522 -1.091 0.281 -1.618 0.480
x1 0.7985 0.104 7.681 0.000 0.589 1.008
==============================================================================
Omnibus: 0.680 Durbin-Watson: 2.345
Prob(Omnibus): 0.712 Jarque-Bera (JB): 0.342
Skew: -0.200 Prob(JB): 0.843
Kurtosis: 3.060 Cond. No. 75.0
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
3.1586748135738
# Definer en x-vektor som dekker datapunktene (i dette tilfellet mellom 4 og 7 cm)
X_plot = np.linspace(4, 7, 300)
# Lag så responsfunksjonen ved å bruke parameterne fra modellen vår
fit = model.params[0] + model.params[1]*X_plot
plt.figure(1, figsize=(8, 4))
plt.clf()
plt.scatter(df[df["species"] == "setosa"].sepal_length, df[df["species"] == "setosa"].sepal_width,label="Iris Data")
plt.plot(X_plot, fit, label="Linear Regression Model", color="red", linewidth=3)
plt.xlabel("sepal length")
plt.ylabel("sepal width")
plt.legend()
<matplotlib.legend.Legend at 0x7ff0940178d0>

xmean = np.mean(X_setosa_sepal_length.squeeze())
rse = np.sqrt(model.ssr/(48))
se_beta1 = (rse*rse)/(np.sum((X_setosa_sepal_length.squeeze()-xmean)*(X_setosa_sepal_length.squeeze()-xmean)))
print("Standard feil beta1 = %.6f"%se_beta1)
Standard feil beta1 = 0.010809
Oppgaven fra forelesning 15. januar stopper her. Vi har ikke gått gjennom hypotesetesting ennå. Koden under er derfor å anse som “work in progress”.
Hypotesetesting#
tval = (model.params[1]-0)/se_beta1
print(tval)
73.8780703215139
import numpy as np
from scipy.stats import t
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 1)
ndf = 50-2
x = np.arange(-100,100,0.001)#np.linspace(t.ppf(0.01, ndf),t.ppf(0.99, ndf), 100)
tsurv = t.sf(x, ndf)
ax.plot(x, tsurv,'r-', lw=5, alpha=0.6, label='t pdf')
[<matplotlib.lines.Line2D at 0x7ff086f8f610>]
tsurv[cutval]
Non dependent variables#
X_setosa_sepal_length = df[df["species"] == "setosa"].sepal_length.to_numpy()
X_versicolor_sepal_width = df[df["species"] == "versicolor"].sepal_width.to_numpy()
plt.scatter(X_setosa_sepal_length, X_versicolor_sepal_width)
X_setosa_sepal_length = X_setosa_sepal_length[:, np.newaxis]
X_versicolor_sepal_width = X_versicolor_sepal_width[:, np.newaxis]
clf = LinearRegression().fit(X_setosa_sepal_length,X_versicolor_sepal_width)
print("Coefficient = %.2f"%clf.coef_)
print("Intercept = %.2f"%clf.intercept_)
print("Score = %.2f"%clf.score(X_setosa_sepal_length,X_versicolor_sepal_width))
X_plot = np.linspace(4, 7, 300)
fit = clf.intercept_[0] + clf.coef_[0]*X_plot
plt.figure(1, figsize=(4, 3))
plt.clf()
plt.scatter(X_setosa_sepal_length,X_versicolor_sepal_width)
plt.plot(X_plot, fit, label="Linear Regression Model", color="red", linewidth=3)
X_versicolor_sepal_width = sm.add_constant(X_versicolor_sepal_width)
model = sm.OLS(X_setosa_sepal_length,X_versicolor_sepal_width).fit()
#display model summary
print(model.summary())
# residual sum of squares
print(model.ssr)
model.params
X_plot = np.linspace(4, 7, 300)
fit = model.params[0] + model.params[1]*X_plot
plt.figure(1, figsize=(4, 3))
plt.clf()
plt.scatter(X_setosa_sepal_length,X_versicolor_sepal_width)
plt.plot(X_plot, fit, label="Linear Regression Model", color="red", linewidth=3)
import numpy as np
from scipy.stats import t
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 1)
ndf = 50-2
x = np.linspace(-1,1,200)
ax.plot(x, t.sf(x, ndf),'r-', lw=5, alpha=0.6, label='t pdf')
tfunc = t.sf(x, ndf)
prob = 0.0
n = -1
for i in x:
n += 1
if i > 0.540:
print(n)
break
tfunc[154]
c = abs(-0.540)
c
tfunc
c = np.arange(0,1,0.1)
csq = c
tail = t.sf(csq,ndf)
fig3, ax3 = plt.subplots(1,1)
ax3.bar(c, tail, color='blue')
ax3.grid(True,axis='y')
ax3.set_xlabel(r'$N$')
ax3.set_ylabel(r'$P(\chi_1^2>N^2$)')
ax3.set_title(r't-stat upper tail probability (p-value)')
ax3.set(xlim=(0, 1))
ax3.set_yscale('log')
yticks = 1/np.power(10,np.arange(1,-1,-1));
ax3.set_yticks(yticks)
plt.show()
tail
0.34546555*2