Exercises

9.1: Sabotage

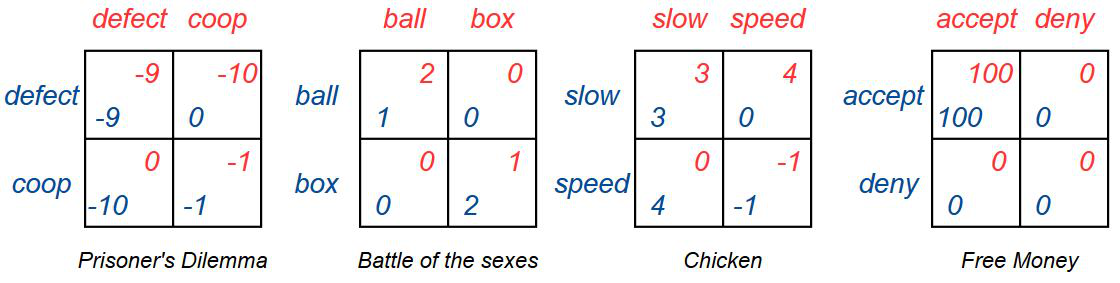
Write a program that given a 2x2 game finds the combination of pure strategies that each player would play to minimize the opponents payoff, where they would not want to change their strategy given what the other player had played.

What does the program give as the preffered strategy for these four games? Compare with the pure strategy nash equilibria for the games and discuss the differences and similarities.

9.2: Pure strategies for larger games

Use best-response analysis to find the Nash equilibria (if plural) in this game. Pen and paper is recommended!

	Left	Middle	Right
North	2,2	7,2	6,3
East	1,2	3,4	3,1
South	7,2	1,3	3,7
West	6,8	6,5	1,2

**9.3: Pure strategies with more players

Three students are preparing for their exams. Prima and Secundus would both like to do well, but they struggle with focusing on the work when alone. They could work at home, and get a bit of work done, or go to the university library and get even less work done alone due to the added transport time (in this hypotethical scenario, all students have decent facilities for working at home). If they were to go to the library and collaborate with a student who helps them focus, they would get much more work done, as they themselves are able to help another student focus, just not themselves.

Tertus prefers doing well on the exam to doing poorly - but mostly, he just wants hang out with his co-students. If he joins the group at the library, they will be distracted from work.

With P&S knowing that they won’t resist having fun procrastinating with their friend and will regret if this impacts their grade, and T knowing he’ll have fun but rather not enjoying the library alone, the expected payoffs for the players are given below. The payoffs are in the order Prima, Secundus, Tertus, Primas choices are rows, Secundus choices are columns, and Tertus choices are the different tables.

Tertus Go
	Go	Stay
Go	2,3,10	1,4,6
Stay	3,0,5	3,4,-1

Tertus Stay
	Go	Stay
Go	10,11,2	0,4,2
Stay	3,0,2	3,4,2

Use best-response analysis to find at least one Nash equilibrium. Pen and paper is recommended!

Stay, Stay, Stay is the only nash equilibria.

9.4: Discuss

Game theory studies games. What is a game?

What is a rational agent in game theory?

What is a payoff? A util?

How do these four concepts relate?

What are zero sum games, and why are most actual games not zero sum?

What is a Nash equilibrium?

Why is the rational strategy sometimes to not pick some singular best choice, and instead randomize between options?

What is the difference between a sequential game and a simultaneous game? What is a game of perfect information? What is a dominant strategy? What is subgame perfection?

What is the method for solving a sequential game?